5.1 Basic Terminologies
- Graph - is a collection of nodes/vertices and edges, $G = (V,E)$.
- Undirected Graph - If for each node $V_{i}$ that is connected to $V_{j}$, both $E_{ij}$ and $E_{ji}$ exists. We can connect both nodes with a single undirected edge such that robot can traverse from $V_{j}$ to $V_i$ and $V_i$ to $V_j$. Such graph is called undirected graph.
- Directed Graph - If for each node $V_{i}$ that is connected to $V_{j}$, only $E_{ij}$ exists i.e. the robot can only traverse from $V_i$ to $V_j$. Such graph is called directed graph.
- Path - in a graph is a sequence of nodes $V_i$ such that for adjacent nodes $V_{i+1}$ are connected.
- Cycle - is a path of $n$ nodes, where $V_1 = V_n$.
- Tree - is a directed graph with no cycles.
- Root - is a special node which has no incoming edges.
- Leaf - is a node with no children.
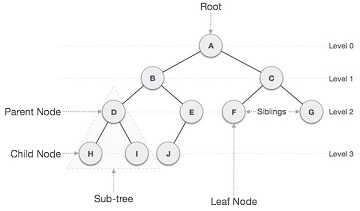
Figure 5.1 Tree
- Grid - induces a graph where each node corresponds to a pixel and an edge connects nodes of pixels that neigbhour each other.
- Four-point connectivity- assumes only four neigbhours i.e. the robot has a choice of moving to one of the four neigbhours at a time.
- Eight-point connectivity- assumes eight neigbhours i.e. the robot has a choice of moving to one of the eight neighbours at a time.

Figure 5.2 8-point and 4-point connectivity
5.2 Depth-First vs Breadth-First Search
- Depth-First Search - starts at the root, chooses a child, then that node’s child and so on until finding either the desired node or a leaf.
- Breadth-First Search - is the opposite of Depth-First. The search starts at the root and then visits all the children of that root first. Next, the search then visits all of the grandchildren, and so forth.
In the following figure, the numbers on each node represents the order in which the nodes are expanded in the search.
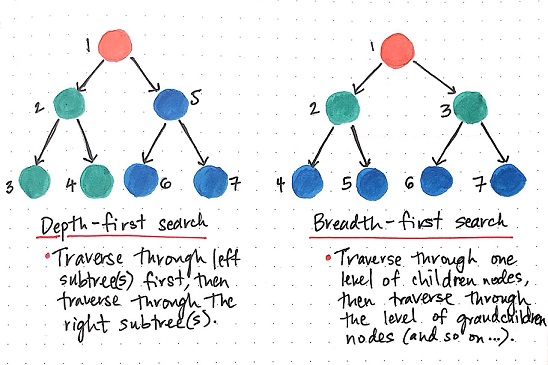
Figure 5.3 Depth-First and Breadth-First Search
5.3 Wave-Front Planner
Wave-Front Planner is a typical example of Breadth-First Search. It is the simplest solution to local minima problem that we encountered in potential functions. However, it can be only implemented in spaces which are represented as grids. Initially, the planner regards free space to a value zero and ones to the obstacles.
Steps:
Given a goal and start position.
- Firstly, the goal pixel is labeled with two.
- All zero-valued pixels or free space neighbouring the goal are labeled with three.(Assume four-point connectivity)
- Next, all zero-valued pixels adjacent to threes are labeled with four.
This procedure essentially grows a wave-front from the goal where at each iteration, all pixels on the wave front have the same path length, measured with respect to the grid, to the goal. This procedure terminates when the wave front reaches the pixel that contains the robot start location. A visualization of the wave-front planner can be seen in the Figure 5.4.

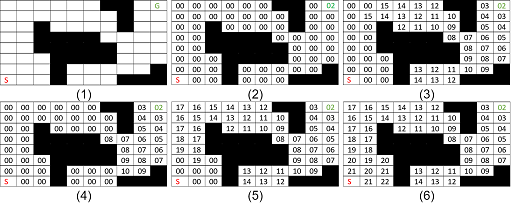
Figure 5.4 Wave-front Planner at random iterations
5.4 Conclusion
- The wave-front planner essentially forms a potential function on the grid which has one local minimum and thus is resoultion complete. The path can be found by following the -ve gradient of this function i.e. towards lower value. Finally, the wave-front planner generalizes into higher dimensions as well. For a three-dimensional space, there will be a three-dimensional pixel or voxel(with six faces).
- It requires a lot of storage and time, which also increases exponentially with increasing dimensions. One can also observe that it explores/expand uniformly i.e. it doesn’t take any advantage of the prior information about start position. In the next post we will see how we can use this information to explore faster.
</> GitHub
5.5 References
[1]. Choset H., Lynch K. M., Hutchinson S. Kantor G., Burgard W., Kavraki L. E., Thrun Sebastian. Principles of Robot Motion. MIT Press
[2]. RI16-735 Robot Motion Planning - link
Bonus!
- In two-dimension, let’s take four-point or eight-point connectivity. Similarly, what will be the connectivity in voxel(three-dimensional)?